A Piece Of Glass Is Broken Into Two Pieces Of Different Size. How Do Their Densities Compare?

Drinking glass Density Evidence

Last updated
Save as PDF

Page ID: 50013

Chemical Education Digital Library (ChemEd DL)

Sometimes identifying i type of glass or glass fragment at a criminal offence scene may be critical in solving a crime, simply the largest database [1] includes 304,107 glass compositions, and so identifying ane of them can be daunting. Although chemists can identify glass by more conclusive methods involving elemental analysis, density may still be used every bit a screening method, as FBI documents indicate FBI Glass Density

Density can exist used to identify smashed glass at the scene of a criminal offence.

Densities of dozens of glasses are known [1]. The most common blazon of glass is ordinary window or bottle glass. It's called soda-lime glass because it is fabricated of sodium carbonate (Na₂CO₃) and CaO (calcium oxide or lime) in improver to silica (sand or quartz, (SiO₂). Pyrex (the Corning make of borosilicate glass, nigh 70% silica, 10% boron oxide (B₂O₃), 8% sodium oxide, 8% potassium oxide, and one% calcium oxide).

Glass densities are determined past an ASTM standard method involving flotation in liquids ^[3], but the density of glass fragments tin also be measured past water displacement, as described below.

The ASTM floatation method is interesting. A layer of "heavy" bromoform is commencement added to a cylinder. It has a density of 2.889 g/cm³ at 15 °C, so near mutual glasses will float on its surface. Next, a layer of 20% ethanol in bromoform is carefully floated on the bromoform. Ethanol is light, having a density of 0.789 g/cm^three, so when it's mixed with bromoform, the resulting solution is just a bit denser than bromoform. Layers of twoscore%, 60%, and fourscore% ethanol in bromoform, followed past 100% ethanol are added, and the layers are allowed to sit down overnight. They diffuse into one some other, giving a gradually changing density from 0.789 to 2.889 thousand/cm³. When glass pieces are added, they bladder at the level where the density matches. A density gradient column can exist created with carbohydrate solutions in dyed water ^[4], as shown in the effigy.

Density Gradient

The terms heavy and low-cal are commonly used in 2 unlike ways. We refer to weight when we say that an adult is heavier than a child. On the other hand, something else is alluded to when we say that flint optical glass is heavier than ordinary bottle glass. A small shard of flint would obviously counterbalance less than a gallon glass jug, but flint is heavier in the sense that a piece of given size weighs more than the same-size piece of bottle glass.

What we are actually comparing is the mass per unit of measurement volume, that is, the density. In club to determine these densities, we might weigh a cubic centimeter of each type of glass. If the flint sample weighed 7.2 g and the bottle drinking glass 2.iv g, nosotros could describe the density of flintstone equally 7.2 thousand cm^–3 and that of bottle drinking glass equally two.4 chiliad cm^–3. (Note that the negative exponent in the units cubic centimeters indicates a reciprocal. Thus 1 cm^–3 = 1/cmⁱⁱⁱ and the units for our densities could be written as 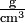, grand/cmⁱⁱⁱ, or one thousand cm^–iii. In each instance the units are read equally grams per cubic centimeter, the per indicating sectionalisation.) Nosotros often abbreviate "cm^three" as "cc", and 1 cm³ = 1 mL exactly by definition.

Table \(\PageIndex{1}\) Density of Diverse Materials
Glass Blazon	Density/g/cm³
sand	1.52
fused silica (96%)	2.18
Corning Vycor® 7907 UV-Blocking Drinking glass	2.21
Pyrex(R)	2.23
borosilicate glass	ii.4
ordinary bottle	~2.4-two.eight
ordinary window	~2.4-two.8
Corning 0211 Zinc Borosilicate Glass	two.53
Corning 1724 Aluminosilicate Crushed/Powdered Glass	ii.64
crown glass	2.8
Corning 0159 Lead Barium Crushed/Powdered Glass	three.37
pb crystal	3.i
Corning 8870 Potash Lead Crushed Glass	4.28
densest flintstone optical	7.2
Densities of many more materials are easily constitute

In general it is non necessary to weigh exactly 1 cm^three of a material in society to determine its density. Nosotros only measure mass and book and divide book into mass:

\[\text{Density} = \dfrac{\text{mass}} {\text{volume}}\]

\[\rho = \dfrac{\text{m}} {\text{V}}\]

where ρ = density m = mass V = volume

Example \(\PageIndex{1}\): Density Calculation

Calculate the density of (a) a piece of glass shard whose mass is 37.42 g and which, when submerged, increases the water level in a graduated cylinder by 13.9 ml; (b) a glass cylinder of mass 25.07 g, radius 0.750 cm, and peak 5.25 cm.

Solution

a) Since the submerged metal displaces its own volume,

\[\text{Density} =\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{37.42 1000} {13.9 mL} = \text {ii.69 one thousand/mL or 2.69 1000 mL}^{-1}\]

b) The volume of the cylinder must be calculated offset, using the formula

\[\text{V} = {\pi} r^{2} h = 3.142 × \text{(0.750 cm)}^{two} * 5.25 \text{cm} = \text{9.278 718 8 cm}^{3}\]

And then \[\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{25.07g} {9.278 718 8cm^{3}}\]

\[= \text{2.70} \dfrac{\text{thou}}{\text{cm}^3}\]

Note

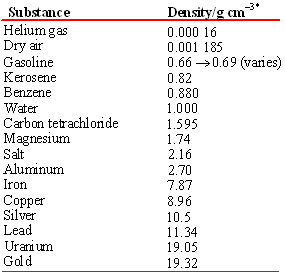
Note that dissimilar mass or volume, the density of a substance is independent of the size of the sample. Thus density is a property by which one substance can be distinguished from another. A sample of glass can be cleaved or adjusted to have whatsoever mass we choose, only its density volition always be 2.lxx g/cm³ at 20°C, so the forensic sample tin can be used to identify the glass canteen from which it was cleaved. The densities of some common pure substances are listed in the Tabular array.

Tables and graphs are designed to provide a maximum of data in a minimum of space. When a physical quantity (number × units) is involved, it is wasteful to keep repeating the same units. Therefore information technology is conventional to use pure numbers in a table or along the axes of a graph. A pure number can be obtained from a quantity if we carve up past appropriate units. For example, when divided past the units gram per cubic centimeter, the density of aluminum becomes a pure number 2.seventy:

\[\dfrac{\text{Density of aluminum}} {\text{1 thou cm}^{-3}} = \dfrac{\text{2.seventy g cm}^{-3}} {\text{1 g cm}^{-3}} = 2.70\]

Tabular array \(\PageIndex{2}\) Density of Several Substances at twenty°C.

Therefore, a column in a tabular array or the axis of a graph is conveniently labeled in the following form:

\[\dfrac{\text{Quantity}}{\text{units}}\]

This indicates the units that must be divided into the quantity to yield the pure number in the table or on the centrality. This has been done in the 2d column of Tabular array 1.iv.

Converting Densities

In our exploration of Density, notice that chemists may express densities differently depending on the subject. The density of pure substances may exist expressed in kg/m^three in some journals which insist on strict compliance with SI units; densities of soils may be expressed in lb/ft³ in some agricultural or geological tables; the density of a cell may be expressed in mg/µL; and other units are in mutual use. It is easy to transform densities from ane gear up of units to another, by multiplying the original quantity past one or more unity factors :

Case \(\PageIndex{2}\): Density Conversion

Convert the density of water, 1 g/cm^three to (a) lb/cm³ and (b) lb/ft³

a. The equality 454 g = 1 lb tin be used to write two unity factors,

\(\dfrac{\text{454 g}} {\text{ane lb}}\) or \(\dfrac{\text{1 lb}} {\text{454}}\)

The given density tin be multiplied by 1 of the unity factors to become the desired upshot. The correct conversion factor is chosen so that the units cancel:

\(\dfrac{\text{one g}} {\text{cm}^{3}}* \dfrac{\text{1 lb}} {\text{454 chiliad}} = \text{0.002203} \dfrac{\text{lb}} {\text{cm}^{iii}}\)

b. Similarly, the equalities two.54 cm = one inch, and 12 inches = ane ft can be use to write the unity factors:

\(\dfrac{\text{2.54 cm}} {\text{ane in}}\), \(\dfrac{\text{1 in}} {\text{2.54 cm}}\), \(\dfrac{\text{12 in}} {\text{ane ft}}\) and \(\dfrac{\text{1 ft}} {\text{12 in}}\)

In society to convert the cm³ in the denominator of 0.002203 \(\dfrac{lb} {cm^{three}}\) to inⁱⁱⁱ, we demand to multiply by the appropriate unity factor three times, or past the cube of the unity factor:

\(\text{0.002203} \dfrac{\text{m}} {\text{cm}^{three}}\) 10 \(\dfrac{\text{2.54 cm}} {\text{ane in}}\) ten \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) ten \(\dfrac{\text{ii.54 cm}} {\text{1 in}}\)

\(\text{0.002203} \dfrac{\text{m}} {\text{cm}^{3}}\) ten \((\dfrac{\text{2.54 cm}} {\text{1in}})^{3} = \text{0.0361} \dfrac{\text{lb}}{\text{in}^iii}\)

This can and so be converted to lb/ft³:

\(\text{0.0361} \dfrac{\text{lb}} {\text{in}^{three}}\) 10 \(\dfrac{\text{12 in}} {\text{ane ft}})^{3} = \text{62.4} \dfrac{\text{lb}}{\text{ft}^3}\)

Note

It is important to observe that we have used conversion factors to catechumen from 1 unit to another unit of measurement of the same paramter .

From ChemPRIME: 1.viii: Density